Come suonare la sequenza di Fibonacci

La successione di Fibonacci è una sequenza di tipo matematico per la quale, posti dei numeri interi positivi, ogni numero risulta essere la somma dei due numeri che lo precedono. Tutto chiaro? Se così non fosse basta dare un occhio ai primi termini della successione per avere un quadro più definito: 1, 1, 2, 3, 5, 8, 13 e... 21 ovviamente (13 + 8), e via così all'infinito.

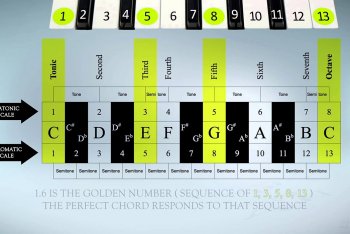
La successione prende il nome dal matematico Leonardo Pisano, detto Fibonacci, figura importantissima per la diffusione della matematica in Occidente. Un tipo di successione così armonica non poteva non avere anche una sua natura melodica. Come da regola infatti: "si dice che i numeri della successione di Fibonacci tradotti nelle sette note musicali danno luogo a una melodia di sedici note che va ripetendosi all’infinito – sempre identica a se stessa – col vertiginoso e spiraliforme progredire della successione".

Come fare? Assegnando ad ogni numero una nota musicale (DO=1, RE=2, etc.) e utilizzando un'operazione di modulo (per adeguare i numeri alle sette note) otteniamo una sequenza di numeri che possono essere trasformati nelle nostre sette note.

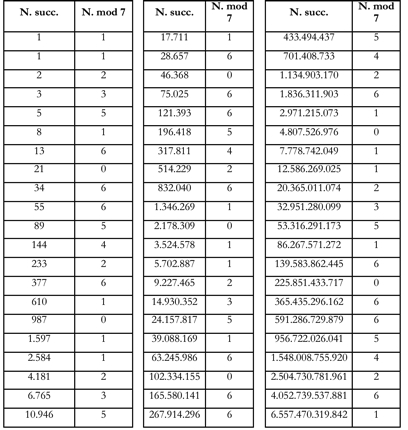
La sequenza di note si ripete identica ogni 16 note, lasciandoci così in mano una melodia ricorsiva, un piacevole divertissment da suonare a piacimento. Tra i musicisti ad utilizzare questo gioco armonico ci sono i Tool, nella title-track di "Lateralus" (qui trovate una spiegazione esauriente), ma girando su YouTube si trovano altri vari esempi che testimoniano come suonare la matematica sia (quasi) sempre possibile.

[via]

---
L'articolo Come suonare la sequenza di Fibonacci di Marcello Farno è apparso su Rockit.it il 2016-02-18 11:41:00